NMR Experiment Index and Fundamentals
Experiment Index
NMR Processing
Books and Resources
- P.J. Hore
- J. Keeler, Understanding NMR Spectroscopy
- Keeler Group Lectures
- Spin Choreography
- Fundamentals of protein NMR spectroscopy
- Predicting NMR Parameters from Molecular Structure
Basis of NMR
Motion in a Circle
-
Radians and Frequency
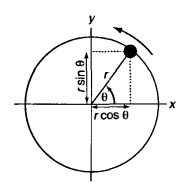
- x-component:
- y-component:
- The x and y components can be plotted against
(in radians). 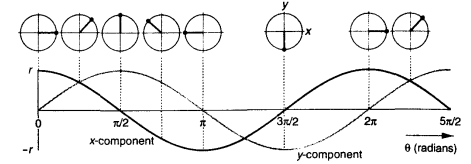
- Frequency:
(Hz) - Angular Frequency:
(rad/s) - Relationship:
-
Phase
- The phase is how far along an oscillation we have proceeded,
. - Phase after time
: - Example:
- If
, the y component is a cos wave, and the x component is a -sin wave. 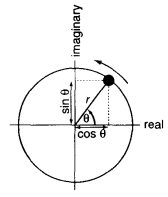
- If
- Complex Number Representation:
- Position at time
: - If phase at
is :
- Position at time
- The phase is how far along an oscillation we have proceeded,
Energy Level Model
-
Energy Differences
- Photons can only be absorbed if
- The NMR spectrum has lines at frequencies depending on the energy separation between levels.
- Transitions between energy levels are allowed if they satisfy quantum mechanical selection rules.
-
Why the Energy Level Approach Is Flawed
- Molecules are not confined to one energy level and can exist in superposition states.
- Mixed states of vibrational and electronic energy levels in IR and UV-Vis have short lifetimes due to molecular collisions.
- NMR differs as nuclei are less affected by collisions, and we can manipulate states using RF pulses.
-
The Hamiltonian and Energy Splitting
- The Hamiltonian (
) gives the energy observable. - Example for one nuclear spin in a magnetic field
: - For
: eigenfunctions are and
- The energy of allowed transitions can be calculated, e.g., Lamor frequency
.
- The Hamiltonian (
Rotating Frame of Reference
-
Concepts
-
Precession
- Vector model for magnetization.
- Precession at the Lamor frequency:
-
Pulses
- RF pulses perturb spins when the resonance condition is met.
-
Rotating Frame of Reference
- Simplifies understanding of RF pulses as two counter-rotating fields.
- Effective Field:
-
-
Resonance Pulse
-
On-Resonance Pulse
- Effective field along the x-axis.
- Flip angle
given by
-
Off-Resonance Pulse
- Produces some x-magnetization, reducing signal strength for large offsets.
- Selective Excitation: Transmitter on resonance with the line of interest.
-
Fourier Transform and FID
-
Fourier Transform Basics
- Converts time domain into frequency domain.
- Example formula:
- Free Induction Decay (FID)
- Evolves as
- Decay over time characterized by
.
- Evolves as
-
Lineshape and Phase
- Absorption Mode Lorenzian Lineshape
- Phase Correction
- Zero-Order: Applied to the whole spectrum.
- First-Order: Adjusts phase based on the offset from the transmitter.
Quantum Mechanical Model
- Toolbox for NMR
- Superposition States
- Wavefunction:
- Wavefunction:
- Dirac Notation
- Wavefunctions as "kets"
and their conjugates as "bras" - Integration in Dirac notation:
- Wavefunctions as "kets"
- Normalization and Orthogonality
- Normalized wavefunction:
- Orthogonal eigenfunctions:
- Normalized wavefunction:
- Expectation Value
- Average result from the measurement:
- Example: Expectation value for
:
- Average result from the measurement:
- Superposition States
Two-Site Exchange
-
Symmetrical Exchange
- Slow Exchange:
- Intermediate Exchange:
- Fast Exchange:
- Slow Exchange:
-
Unsymmetrical Exchange
- Determine ratios of compounds in fast exchange using the formula:
- Determine ratios of compounds in fast exchange using the formula:
NMR Timescale
- NMR Timescale Definition
- Ability of the NMR to distinguish between frequencies.
- If chemical exchange is faster than the NMR timescale, signals are averaged.
- A slow or fast process on the NMR timescale is determined by the difference in frequencies of the exchanging sites.
Additional Concepts
-
Spin Echo
- Technique for refocusing spin dephasing.
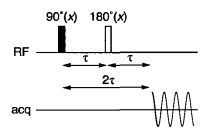
-
Product Operators
- One Spin Operators
- Time evolution and rotation using Hamiltonian and operators.
- Calculation examples provided.
- One Spin Operators
-
Density Operator
- Represents ensemble average and helps compute bulk magnetization.
- Evolution given by the Liouville-von Neumann equation.
Vector Model
- Basis
-
Bulk Magnetization
- Slight alignment of spins in a magnetic field creates bulk magnetization.
- Precession at the Lamor frequency:
(rad/s).
-
Detection
- Precessing nuclei induce a current in the coil, producing the Free Induction Decay (FID).
- A 90-degree pulse shifts magnetization into the xy-plane, which then precesses.
-
Pulses
- To perturb spins, RF pulses are applied, aligning with the resonance condition.
- The Rotating Frame of Reference simplifies understanding of pulses as rotating fields.
-
Effective Field:
-
On-Resonance Pulse: Effective field along x-axis.
-
Off-Resonance Pulse: Creates x-magnetization, reducing signal strength for large offsets.
-
Quantum Mechanical Model: Detailed
-
Quantum Chemistry Toolbox for NMR
-
Superposition States
- Wavefunction of a spin as a superposition of eigenfunctions:
.
- Wavefunction of a spin as a superposition of eigenfunctions:
-
Dirac Notation
- Wavefunctions are "kets"
, their conjugates are "bras" . - Integration:
.
- Wavefunctions are "kets"
-
Expectation Value
- Average result of measurements:
. - Example for
: .
- Average result of measurements:
-
Matrices and Pauli Matrix
- Matrix representation:
. - Example for
: .
- Matrix representation:
-
-
Bulk Magnetization Computation
-
Ensemble Average
- Bulk magnetization as the sum of individual spin magnetic moments.
- $M_z = {\gamma N \overline {\langle I_z\rangle}} $ where
is the ensemble average.
-
Expectation Value and Population
- Expectation value
relates to the population of spin states.
- Expectation value
-
Time Evolution
- Time-Dependent Schrodinger Equation (TDSE)
- Time evolution of wavefunction:
. - Free Evolution: When no RF field is present,
.
- Time evolution of wavefunction:
- Time-Dependent Schrodinger Equation (TDSE)
-
RF Pulses
- On-Resonance Pulse:
. - Effect on Angular Momentum: Calculation of expectation values for x, y, z components during a pulse.
- On-Resonance Pulse:
-
Density Operator
- Liouville-von Neumann equation:
. - Equilibrium Density Operator:
, leading to simplified calculations of bulk magnetization.
- Liouville-von Neumann equation:
-
Product Operators
- Example of time evolution and rotation using Hamiltonian and operators.
-
-
Spin Echo
- Technique for refocusing spin dephasing using pulses and delays.

Fourier Transform and Signal Processing
-
Fourier Transform
- Converts the time domain (FID) into the frequency domain.
- Example:
.
-
Free Induction Decay (FID)
- Describes how the signal decays over time, usually characterized by
relaxation time. - The FID can be manipulated using weighting functions to enhance sensitivity or resolution.
- Describes how the signal decays over time, usually characterized by
-
Phase and Lineshape
- Absorption Mode Lorenzian Lineshape: Standard form in NMR spectra.
- Phase Correction: Adjustments for phase errors, including zero-order and first-order corrections.
-
Manipulating FID and Dealing with Noise
- Techniques include Zero-Filling, Weighting Function, and Acquisition Time adjustments.
- Strategies to enhance sensitivity and resolution, such as the Lorentz to Gauss transformation and Sine-Bell Functions.
This note preserves all the detailed content while organizing it into clear, logical sections. Each section is easy to navigate and reference, maintaining the complexity and depth of the original content while enhancing readability and usability in Obsidian.