-
TLDR
- Cyclic Voltamogram Breakdown:
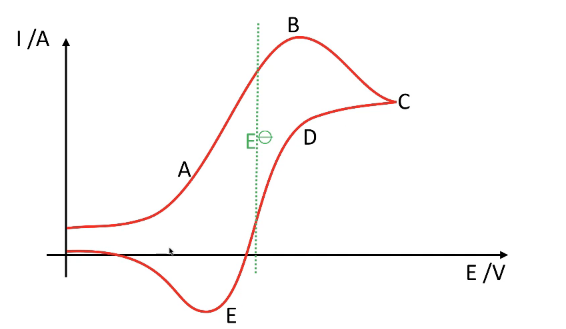
- A - Low potential oxidation sweep:
- Current rises as anions are oxidized.
- Rate limited by ion migration.
- Diffusion of oxidized species is faster than ion migration. The diffusion layer remains constant.
- Electrochemical control is taking place.
- B - High potential oxidation sweep:
- Oxidation current reaches maximum.
- Migration of anions equals diffusion rate.
- The diffusion layer grows as ions are oxidized faster than they arrive at the electrode, causing current to drop off.
- C - High potential turning point:
- Surface saturated with oxidized species.
- Anion approach hindered.
- Rate limited by diffusion of oxidized species.
- D - High potential reduction sweep:
- Surface still saturated with oxidized species which rapidly reduce.
- Current flows in the opposite direction.
- E - Low potential reduction sweep:
- Overall current minimum.
- Diffusion of oxidized species faster than ion movement.
- Cyclic Voltamogram Breakdown:
-
Theoretical Concepts
-
Faradaic current vs. non-Faradaic current
- non-Faradaic current: Current generated by processes that do not involve electron transfer between the electrode and solution.
- Faradaic current: Processes that involve heterogeneous electron transfer, such as redox reactions between the electrode and solution.
- Example:
- If no redox active species are present: A current flows briefly due to solvent reorganization, then stops.
- If redox active species are present: Additional current flows for a longer time, depending on the net rate of diffusion of the redox species to the electrode and the applied overpotential.
-
The Three Electrodes
- Significant current flowing through two electrodes complicates accurate potential difference measurement.
- The Counter electrode allows current flow, measuring the current, while the Reference electrode measures potential.
- The surface area of the Counter electrode is much larger than that of the Working electrode to ensure the current rate-limiting step occurs at the working electrode.
- Depolarizing reactions at the CE, like H
+ e H , are typically ignored but should be fast compared to the WE processes. 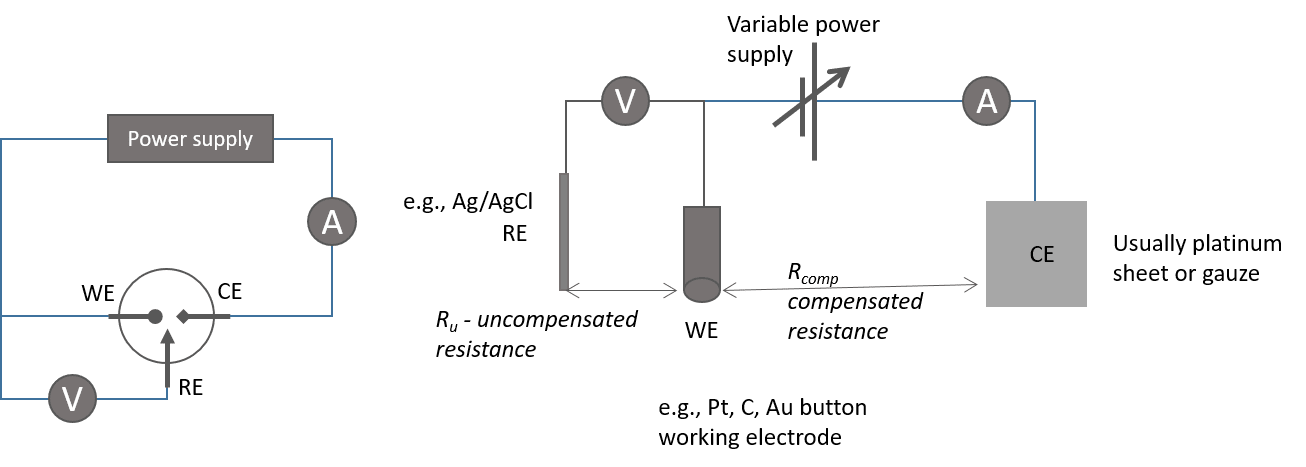
- Depolarizing reactions at the CE, like H
- Reference electrode Ag-AgCl:
- The AgCl electrode is an almost ideal non-polarizable electrode, maintaining its state through oxidation or reduction.
- This fails when the current exceeds the electron transfer rate, causing depolarizing reactions to lag.
- Oxidized and reduced forms must be available to counteract polarization.
-
Cell resistance and Time constant (RC)
- Large iR drop with poorly conducting solvents must be compensated electronically.
- Fully or partially dissociated salts improve conduction.
- If resistance is present, the measured potential differs from the actual (
) potential: - The capacitance and time constant of the cell also need to be considered:
, where (time constant). - When the double layer becomes charged,
becomes long, then .
- Temperature change due to resistive heating must also be considered for high-current and potential applications.
- The time constant can be reduced by:
- Decreasing the double layer capacitance
by using a smaller electrode, e.g., Micro-electrode, since capacitance is proportional to area. - Increasing solution conductivity by adding electrolyte and increasing solvent polarity.
- Decreasing
by positioning the RE close to the WE, as resistance is proportional to distance. - Decreasing analyte concentration, hence decreasing Faradaic current.
- Decreasing the double layer capacitance
-
Current Response to Potential Steps and Ramps Capacitance
- In the absence of redox species:
- A change in electrode potential should result in little or no current change, but solvent reorganization causes a transient current flow.
- The RC time constant must be considered as it takes time for the system and solvent molecules to reorganize.
- If potential changes smoothly, the double layer reorganizes continuously, resulting in a steady current flow.
- If potential changes in the opposite direction, current flows in the opposite direction.
- The double layer capacitance
counteracts polarization, and current is related to the movement of charge : , hence , where is the rate of change of potential in . 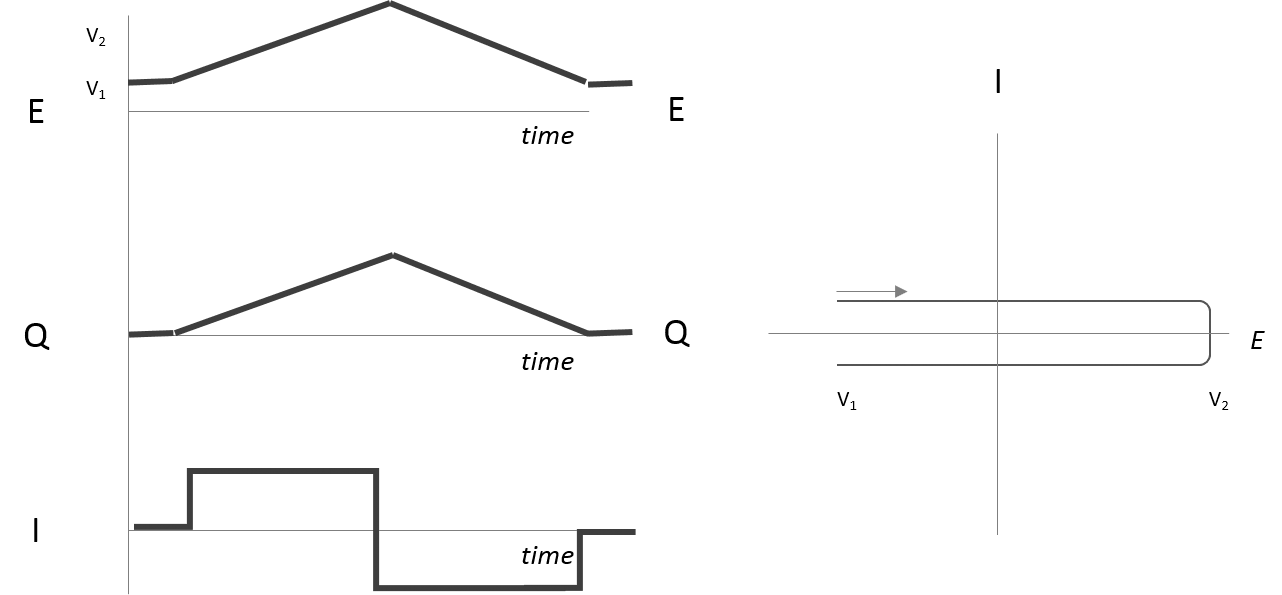
- In the presence of redox active species adsorbed to the surface:
- At any initial potential
, the concentration of oxidized and reduced species adsorbed to the electrode follows the Nernst Equation. - If
is negative compared to the equilibrium potential, the redox active species is in the reduced state. - A sudden step potential change disrupts the redox ratio, and equilibrium is restored by electron transfer.
- At any initial potential
- Current Response to a Linear Potential Sweep with Redox Active Species Adsorbed to the Surface:
- A steady current due to double layer charging is observed when
is far from the equilibrium of the species. - The shape of the voltamogram can be predicted using the Nernst Equation:
- The current at any potential is proportional to the surface concentration
, the number of electrons transferred per mole of reactant, and the electrode area: - We can use the Nernst equation to calculate
: , which rearranges to:
- Since
, then:
- After a series of algebraic arrangements:
- The rate of change of
with time: - Using differentiation by parts and taking into account that
, we obtain a formula for the current: - Peak currents are recorded when
: is the total surface concentration in mol cm . - The area under the redox wave is:
- Therefore, CV can determine surface density for a redox active species.
- The current at any potential is proportional to the surface concentration
- A steady current due to double layer charging is observed when
- Current Response to a Potential Step for Redox Species (Both Red and Ox Soluble):
- The redox active species is present in solution in both oxidized and reduced states.
- The ratio of reduced and oxidized forms in solution is determined by the electrode potential via the Nernst Equation:
- The concentrations of oxidized and reduced forms in the bulk solution may differ from those at the electrode and the edge of the depletion layer.
- The development of a steady-state concentration gradient between the electrode and the edge of the stagnant layer takes time, similar to the scan rates.
- Conclusion: Low scan rates should first be examined to ensure a depletion layer at all times (simpler math).
- In the absence of redox species:
-
Linear Sweep Voltammetry at Low Scan Rates
- When an electrode is at equilibrium at a certain potential
, the concentration of species at the electrode-solution interface satisfies the Nernst Equation. If Ox and Red concentrations are equal, no current flows. - This potential is called the Open Circuit Potential (OCP).
- Consider when only the reduced form is present: [Red] >> [Ox], so the OCP is negative (from Nernst Equation).
- Changing the applied potential to a less negative overpotential but still far from the redox couple's equilibrium, the current is primarily due to double layer charging, with minimal change in reduced and oxidized form concentrations at the electrode.
- Changing the potential in a single step to a positive overpotential
, the concentrations of oxidized and reduced forms at the electrode no longer satisfy the Nernst Equation, and current flows to restore equilibrium. - Initially, concentration changes only occur near the electrode, growing until the Nernst diffusion layer is re-established.
- The net rate of electron transfer depends on the net flux of reduced species diffusing towards the electrode and oxidized species diffusing away.
- Assuming equal diffusion coefficients for Ox and Red, the rate of electron transfer is proportional to the concentration gradient at the electrode (x=0), the number of electrons transferred (n), F, and A:
- When an electrode is at equilibrium at a certain potential
-
Cottrell Equation - Describes the Current Response to a Potential Step Function and Concentration
- Justification:
- For a large area electrode, the rate of change of concentration
depends on the diffusion coefficient of the species and can be predicted at any distance from the electrode and time by considering Fick's laws of diffusion: - At any electrode potential, the equilibrium concentrations of the redox active species at the electrode can be calculated using the Nernst Equation:
- The net flux of red = - net flux of Ox.
- For a large area electrode, the rate of change of concentration
- Cottrell Equation:
- The equation describes the change in current at any time during the experiment, particularly the current response when the potential is a step function in time.
- Eventually, current should approach zero, but the diffusion layer does not thicken indefinitely. Once the concentration gradient relaxes to the thickness of the stagnant layer (
), it no longer decreases. - Ultimately, the current remains constant, dictated by the net diffusion rate between the bulk solution and the electrode, no longer time-dependent.
- Current is time-dependent, allowing determination of diffusion coefficients with Chronoamperometry.
- Summary: The Cottrell equation describes the response of a system with diffusion in solution to a potential change.
- Justification:
-
Increased Scan Rates
- Increasing the potential faster than the diffusion layer can develop affects current.
- A fast overpotential increase oxidizes reduced species rapidly, growing the depletion layer and reducing the concentration gradient.
(concentration gradient) depends on overpotential. - If overpotential increases faster than the diffusion layer forms,
increases as reduced species oxidize faster, lowering Red concentration at the electrode until it reaches 0 (maximal concentration gradient). - Thereafter, the concentration gradient decreases as the diffusion layer thickens, causing
to stabilize. - The peak current scanning towards positive is
and towards negative is . - The peak potential can be predicted using the Randles-Sevcik equation.
-
Randles-Sevcik Equation
- Faradaic current under diffusion control:
due to insufficient time to establish the Nernst diffusion layer before overpotential (eta) changes. - Faradaic current under surface confinement:
- Electrochemically irreversible under diffusion control:
- non-Faradaic current:
(capacitance) - The Charging current is
, where is the electrode area. is inversely proportional to the square root of the scan rate.
- Faradaic current under diffusion control:
-
Electrochemically and Chemically Reversible
- Electrochemically reversible and Chemically reversible processes:
and should be independent of scan rate.
- Electrochemically irreversible:
- The rate of heterogeneous electron transfer is too low to establish a Nernstian equilibrium at the electrode at all times.
- For electrochemically irreversible processes:
is the number of electrons in the process, while is the number of electrons in the rate-limiting step. - Irreversibility can be due to the reaction or electrode cleanliness (e.g., glassy carbon electrode binding COO- groups, repelling electrons).
- If
, the system is electrochemically irreversible. - Sometimes, if
, it may still be irreversible due to a low (e.g., redox active species deep in a protein).
- Quasi-reversible electrochemical systems depend on the rate constant for heterogeneous electron transfer
. At low scan rates, behavior appears normal, but at high scan rates, the system cannot fully respond to potential changes. - Electrochemically reversible step (fast electron transfer rate) has the same
at every scan rate. - The electron transfer rate constant is fast, making analyte diffusion the rate determiner. The concentration rate build-up is almost instant, so no delay in reading, and the same potential is recorded at different scan rates.
- As scan rate increases, the concentration gradient increases, resulting in an increase in
.
- Electrochemically irreversible step (slow electron transfer rate) shows a deviation in
at higher scan rates. - The system takes longer to react (bigger gradient) as scan rate increases, causing more deviation in
.
- The system takes longer to react (bigger gradient) as scan rate increases, causing more deviation in
- Electrochemically reversible and Chemically reversible processes:
-
-
Experimental Concepts and Analysis
-
Deviations from Theory: Differences between
and due to: - Differences in diffusion coefficients of oxidized and reduced forms.
- Kinetics of electron transfer.
- Solution equilibria.
- Irreversibility.
-
Peak Current
- Faradaic current under diffusion control:
due to insufficient time to establish the Nernst diffusion layer before overpotential (eta) changes. - Faradaic current under surface confinement:
- Electrochemically irreversible under diffusion control:
- non-Faradaic current:
(capacitance)
- Faradaic current under diffusion control:
-
Electrochemical Reversibility
- Electrochemically reversible step: (fast electron transfer rate) has the same
at every scan rate. - The electron transfer rate constant is fast, making analyte diffusion the rate determiner. The concentration rate build-up is almost instant, so no delay in reading, and the same potential is recorded at different scan rates.
- As scan rate increases, the concentration gradient increases, resulting in an increase in
.
- Electrochemically irreversible step: (slow electron transfer rate) shows a deviation in
at higher scan rates. - The system takes longer to react (bigger gradient) as scan rate increases, causing more deviation in
.
- The system takes longer to react (bigger gradient) as scan rate increases, causing more deviation in
- Totally Electrochemically irreversible processes are limited by the rate of electron transfer, resulting in linear behavior.
- Diagrams:
- Electrochemically reversible step: (fast electron transfer rate) has the same
- Electrochemical asymmetry: Different charge transfer rates in forward and reverse reactions.
-
- ### Potentials and Peak Separation
-
- If
- For a Nernstian 2 electron transfer,
-
-
Definitions
- Uncompensated resistance: The resistance between the RE and WE multiplied by the current between WE and CE, resulting in a difference between the measured and actual potential. It can be reduced by:
- Reducing distance between electrodes.
- Adding more conductive electrolyte.
- Reducing analyte concentration.
- Faradaic current: Processes that involve heterogeneous electron transfer, i.e., redox reactions between the electrode and solution.
- Charging current: Current due to the reorganization of solvent molecules forming IHP and OHP planes upon potential change.
- Ideal non-polarizable electrode: An electrode with no net DC current between the two sides of the double layer. No Faradaic current exists between the electrode surface and electrolyte, behaving as a capacitor.
- Ideal polarizable electrode: Changes its potential proportionally to the applied charge.
- Uncompensated resistance: The resistance between the RE and WE multiplied by the current between WE and CE, resulting in a difference between the measured and actual potential. It can be reduced by: