Key Definitions

• Symmetry operation: Actions that leave an object unchanged.
• Symmetry element: The axis, plane, or point where a symmetry operation occurs.
• Point group: A set of symmetry operations that describe an object's symmetry.
  • 
• Schoenflies symbols: Symbols denoting a point group.
• Group: A set of elements with the following properties:
  • Associative multiplication: $(a\ast b)\ast c=a\ast (b\ast c)$
  • Closed group: The product of two group elements is within the group.
  • Identity element: An element that leaves other elements unchanged.
  • Inverse element: Every element has an inverse in the group, satisfying $a\ast a^{-1}=e=a^{-1}\ast a$.
• Abelian group: A group where all elements commute, i.e., $ab=ba$. The Character table is symmetric along the diagonal.
• Character table: A table showing the outcomes of all symmetry operation products in a group.
• Class: Symmetry operations that belong to the same class. If $b=c^{-1}ac$, $a$ and $b$ are in the same class.
  • Example: $C_3$ and $C_3^2$ are in the same class since $C_3^2={\sigma }_v^{-1}{C}_3{\sigma }_v$
• Group order: The total number of symmetry operations in a group. The number of Classes can be higher.

Symmetry Operations and Elements

Character Tables

Basic Concepts

• Character tables represent how symmetry operations affect different molecular orbitals or coordinates.
• Irreducible representations are the fundamental blocks of character tables, corresponding to specific symmetry types.
• Mulliken Symbols: Used to label representations in character tables:
  • A: Symmetric with the principal rotation axis.
  • B: Asymmetric with the principal rotation axis.
  • E: Double degenerate.
  • T: Triple degenerate.
  • g/u: Indicate symmetry (gerade) or asymmetry (ungerade) to inversion $i$.
  • Primes and double primes indicate symmetry (prime) or asymmetry (double prime) with respect to ${\sigma }_h$.

Properties of Character Tables

1. The number of irreducible representations equals the number of classes in the group.
2. The sum of the squares of all dimensions of the irreps equals the order of the group.
3. The sum of the squares of all characters of an irrep equals the order of the group.
4. Characters of different representations are orthogonal to each other.

reducible representations

• A reducible representation can be expressed as a sum of irreducible representations (irreps).
• Reduction formula:
  $n_i=\frac{1}{h}{\mathrm{\Sigma }}_R{n}_C{\chi }_{red}(R)\cdot {\chi }_i(R)$
  • $n_i$: Number of times irrep $i$ appears in the reducible representation.
  • $h$: Group order.
  • $n_C$: Coefficient of the respective symmetry element.

Determining Irreducible Representations

Steps to Find an Irreducible Representation

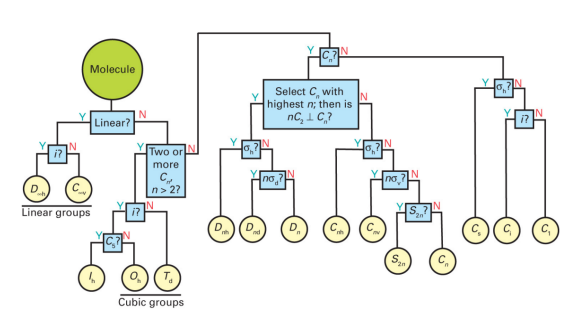
1. Find the point group using flow charts or symmetry elements.
2. Assign x, y, z coordinates to each atom.
3. Determine atomic transformations under symmetry operations:
   • Moving atom = 0
   • Stationary atom = 1 for each unchanged axis, -1 for each inverted axis.
4. Reduce the reducible representation to irreducible components using the reduction formula.

Examples

• N2O4 Example:
  • {{iframe:https://drive.google.com/file/d/1l-tagYBS_2tcHyY-J57SsPd8PMsddhV0/preview?usp=drivesdk}}
• Water Example:
  • 
• Ammonia Example:
  • Source video: {{youtube: https://youtu.be/vxwKbWz0m1o}}
  • 
  • 
• For infinity groups:
  • Solve the problem for a finite subgroup (e.g., C2v instead of C∞v).
  • Use correlation tables to translate Schoenflies symbols to the infinity group.
  • See SF2 Example:
    • 
    • 

Tools and Resources

• Spreadsheet Example: Link to Spreadsheet
• SALCs for Cyclobutadiene: Video Link

Symmetry Adapted Linear Combinations (SALCs)

Building SALCs

1. Find the IRREP.
2. Write the transformation (projection) of basis orbitals.
3. Evaluate each IRREP contributor in terms of basis functions.

Example

• Cyclobutadiene:
  • 

IR and Raman Spectroscopy from Irreducible Representations

Overview

• Normal modes: $3N-6$ for non-linear molecules and $3N-5$ for linear molecules.

Steps to Determine IR and Raman Activity

1. Find the IRREP.
2. Remove irreducible representations for translations and rotations.
3. Determine IR and Raman active modes:
   • IR activity: Requires a change in dipole moment (irreps such as $x,y,z$).
   • Raman activity: Requires a change in polarizability (quadratic functions).

Why Use Symmetry to Predict IR and Raman Modes?

• Normal coordinates and vibrational wavefunctions share symmetry properties, allowing predictions based on the character table.

Example

• Determining the IRREP of a Normal mode:
  • {{iframe:https://drive.google.com/file/d/1W_YAUCjzK-Z9w75jGGe_I1EY8GOr8VGl/preview?usp=drivesdk}}

Electronic Spectroscopy Transitions

• The transition probability for an electronic transition can be determined using the dipole electric moment operator.
  $M_{fi}=⟨f|\overrightarrow{\mu }|i⟩$
• For a transition to occur, the integral must be non-zero. Symmetry considerations can help us determine this.

Steps to Determine Electronic Transitions

1. Determine the molecule point group.
2. Draw or determine orbitals involved in the transition and determine their irreps.
3. Determine the symmetries of different dipole moment operator bases.
4. Find ${\mathrm{\Gamma }}_f{\mathrm{\Gamma }}_{{\mu }_{x,y,z}}{\mathrm{\Gamma }}_i$ for ${\mu }_{x,y,z}$.
5. Transitions are allowed if the result is totally symmetric.

Allowedness of Transitions

• Electronic transition: ${\mathrm{\Gamma }}_f\cdot {\mathrm{\Gamma }}_{{\mu }_{x,y,z}}\cdot {\mathrm{\Gamma }}_i$

  • ${\mathrm{\Gamma }}_{\mu }$ can be any of the irreps related to the $x,y,z$ directions.
  • If the result is or contains a totally symmetric representation, the integral is non-zero, hence the transition is allowed.
  • $A_1, A, A_g, A_{1g}, A^{\prime} $ all give non-zero integrals.
  • The $\mu$ that results in a symmetric representation indicates the required light polarization.

• Vibronic transition: $({\mathrm{\Gamma }}_f\cdot {\mathrm{\Gamma }}_{{\mu }_{x,y,z}}\cdot {\mathrm{\Gamma }}_i)\cdot {\mathrm{\Gamma }}_{\nu }$

  • When an electronic transition is not allowed, a vibrational mode may make it allowed.
  • The symmetry species of the mode multiplies the outcome of the electronic transition.
  • If totally symmetric symmetry is found, the transition is vibronically allowed.

Example

• Vibronic Transition Example:
  • {{iframe:https://drive.google.com/file/d/1qmOi3GlnauC76SExiCcNaeq6r_fkXe-7/preview?usp=drivesdk}}

Translational Symmetry

Crystal Lattice

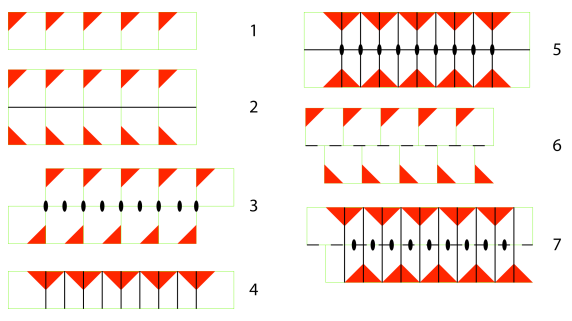
• 1D Lattice:

  • There are 7 types of symmetry.
  • 

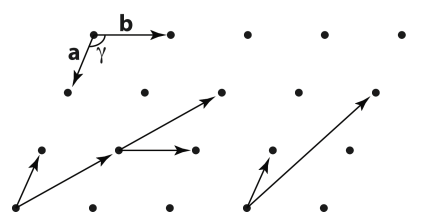
• 2D Lattice:

  • Any pair of non-collinear translation vectors can be used to generate the lattice from one point.
  • There are 5 types of symmetry classes for a 2D lattice.
    •